Solving Sudoku puzzles can be a lifetime activity for everyone! Aside from being just simply fun, it has benefits for people of all ages. Young people have the opportunity to learn problem solving and to concentrate for extended periods of time. For those who are in the workforce, Sudoku is a great companion when traveling, as well as a way to unwind at the end of the work day. And retirees have a stimulating activity to help keep the mind sharp!

A small amount of history. Seven years ago I did my first Sudoku puzzle. As time progressed I began to attempt puzzles at more challenging levels, some of which I could not solve. Researching Sudoku techniques was frustrating. Most did not appear to be logical or would be difficult to employ in actual puzzles. Rather than give up the game, over the next year I created 3 unique techniques. These techniques have allowed me to “crack” all published Sudoku puzzles! As a consequence I decided to publish and print a book about these techniques, called “3 ADVANCED SUDOKU TECHNIQUES THAT WILL CHANGE YOUR GAME FOREVER.”
A game of logic. Some people think you have to be a math whiz to be good at Sudoku. Actually you could use the letters A through I, versus 1-9. This game is simply a game of logic!
Rules of the game. Enter the numbers 1 - 9 into the cells such that these numbers do not repeat themselves in a row, column, or box. Additionally, there can be only one solution to a puzzle (this is the basis for step 3 below).
PUZZLE PREPARATION:
1. Fill in all obvious answers, in each of the 9 Boxes.
2. Enter all potential options across the top of the unsolved cells, using pencil.
3. Then use the “magical formula” for solving all puzzles:
This article is about Puzzle Preparation. The next 5 articles will cover steps 1 – 5 in depth.
First, let’s define some terms:
- A Cell is an individual box. The puzzle is comprised of 81 (9x9) cells.
- A Column is the vertical collection of 9 cells, Columns are numbered 1 - 9 as you look left to right.
- A Row is a horizontal collection of 9 cells. Rows are numbered 1 - 9 as you look top to bottom.
- A Box is a group of 9 cells, in a 3 x 3 grid. Boxes are numbered 1 - 9, reading left-to-right and top-to-bottom.
LET’S START
Let’s start with a Sudoku puzzle, Example 1 below, which is an actual puzzle that will be in my second book called “200 SUDOKU PUZZLES THAT REQUIRE DAN’S ADVANCED TECHNIQUES.”
You may want to print Example 1, or copy it onto a blank Sudoku grid, and follow along with your pencil and pen. Use your pen for solved cells and your pencil for all unsolved cells.
We will use an abbreviation for cells; for example Cell C7R1 (column 7, row 1) = 3; C1R5 = 8.
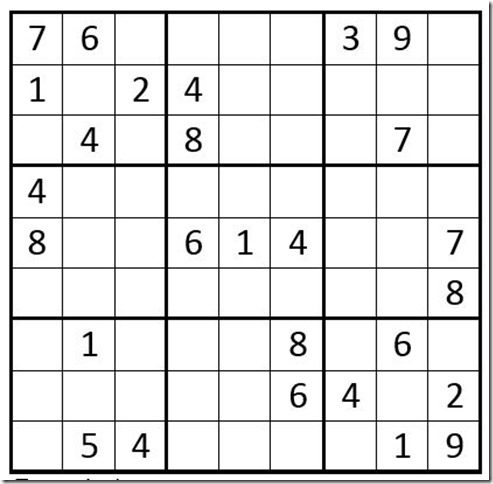
Example 1
|
Begin by filling in all obvious 1-choice answers in Example 1, remembering that within a column, row, or box, there is only one cell that can contain a particular number. Reading above, we will start with boxes; by adding the #’s 1, 2 ... through 9, you will find the following, obvious answers, by comparing each box to the adjacent ones: C4R8 = 1. C7R3 = 2. C8R6 = 4. C9R1 = 4. C5R7 = 4. C1R9 = 6. C5R4 = 8.
By solving these cells, you will have set-up some more obvious, 1-choice cells, which you will find; when you go through #’s 1 - 9 again, you find: C9R3 = 1. C6R1 = 1. C1R7 = 2.
If you review numbers 1 – 9 again, it does not produce any more obvious 1- choice cells. Now your grid should look like Example 2 below …
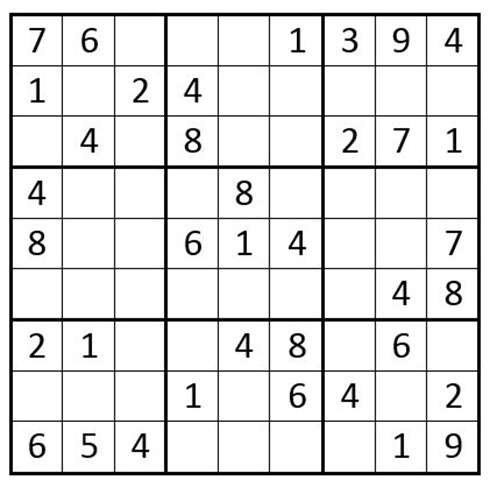
Example 2
|
Next, look for the not-so-obvious, 1–choice cells. Cells C7R2, C8R2, & C9R2 must be some order of the numbers 5, 6, and 8. Therefore C5R2 and C6R2 cannot be a 5, 6, or 8. If we look at the 6’s in box 2, we see that the only remaining cell that can be a 6, is C5R3. So enter a 6 in that cell. Using the same reasoning, C2R2 cannot be a 5, 6, or 8 either. Therefore C3R1 = 8. Then C2R8 = 8, C7R9 = 8, C8R2 = 8, C7R7 = 7, and C3R8 = 7. Now your grid should look like Example 3 below:
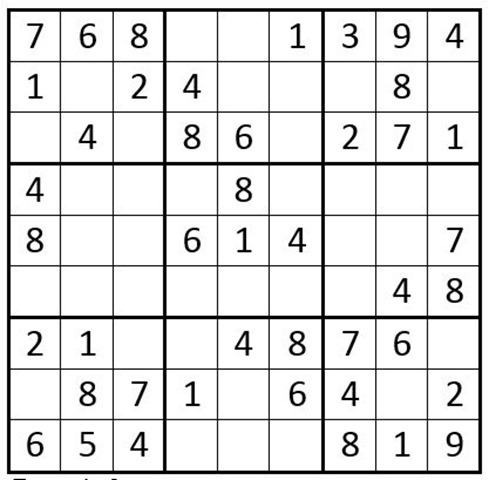
Example 3
|
Indicate options that cannot exist in a cell: C2R9 is a 5, therefore C2R2 cannot be a 5. Similarly, either C1R3 or C3R3 must be a 5, therefore C6R3 cannot be a 5. Normally we would indicate this by writing a small 5 in the bottom of C6R3, however, as you will soon see, this will be remedied in a more encompassing way.
First fill in obvious pairs and triplets.
C4R1 and C5R1 must be a 2 or 5, so we will indicate the options for these cells as “25” in the upper portion of these cells. C7R2 and C9R2 must be a 5 or 6, so indicate “56”. C4R9, C5R9, & C6R9 must be “2, 3 or 7”. Now your grid should look like Example 4 below:
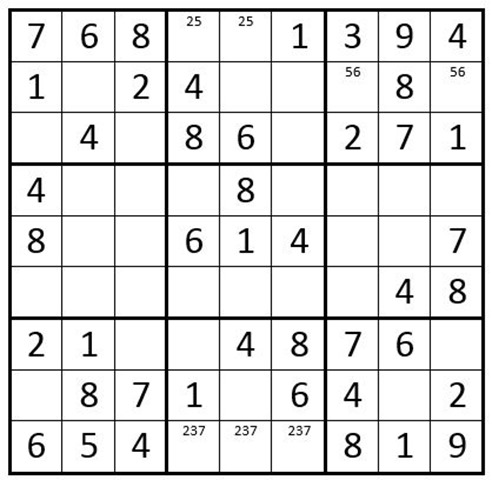
Example 4
|
So why did we just pick those two pair and the triplet? We picked them because they affect other cells. For example, the 25 in C4R1 and C4R2 affect the other cells in box 2. The other 3 unsolved cells in box 2 cannot contain a 2 or 5, and therefore are limited to 3, 7, and 9. Likewise, the 56 in C7R2 and C9R2 preclude the other cells in row 2 from containing a 5 or 6. The triplet in box 8 precludes the other 2 cells from being a 2, 3, or 7, and therefore they are either 5 or 9. So we will fill in the options for the unsolved cells in box 2, row 2, and box 8 first.
Now your grid should look like Example 5 below:
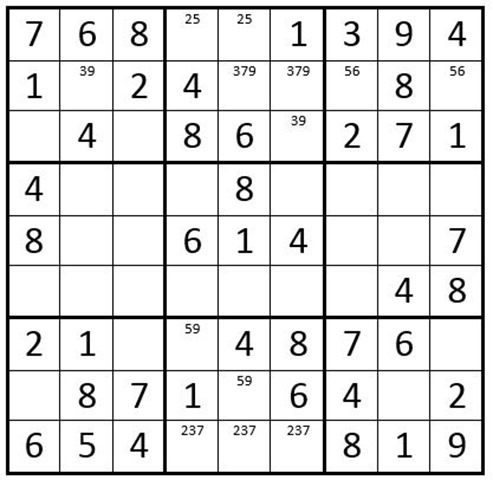
Example 5
|
So why did we not mention the pair in box 7 or box 9? The 2 cells with 39 as their options in box 7, do not influence the options of any other unsolved cells. The same applies for the 2 unsolved cells in box 9.
Next fill in the options for the remaining unsolved cells. Your grid should now look like Example 6 below:
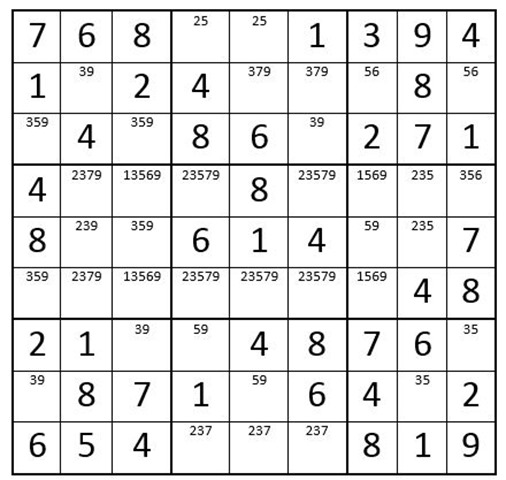
Example 6
|
Now you have completed the puzzle preparation. We will refer to this puzzle in upcoming articles, so please retain your grid.
OK, now it is your turn. For practice, complete the puzzle preparation for Example 7 below (again, you may want to do the puzzle preparation on a blank grid or print this page):
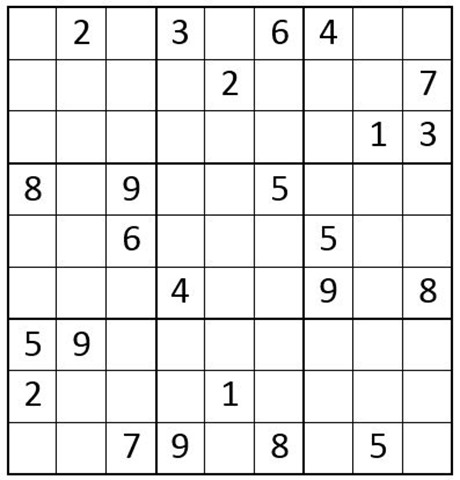
Example 7
|
If you are having problems, you can refer to the puzzle preparation “key” as follows:
1-choice: C3R6 = 2. C7R3 = 2. C9R1 = 5. C4R8 = 5. C5R3 = 5. C2R6 = 5. C3R2 = 5.
Not as obvious 1-choice: C9R8 = 9. C9R9 = 2.
Options that cannot exist in a cell: C1R2 and C2R2 cannot be a 1 or 6. C6R7 and C6R8 cannot be a 4.
Your puzzle preparation should look like Example 8 - with all possible numbers displayed.
Please save this grid for future article techniques.
If you review numbers 1 – 9 again it does not produce any more obvious 1-choice cells. Now your grid should look like Example 8 below …
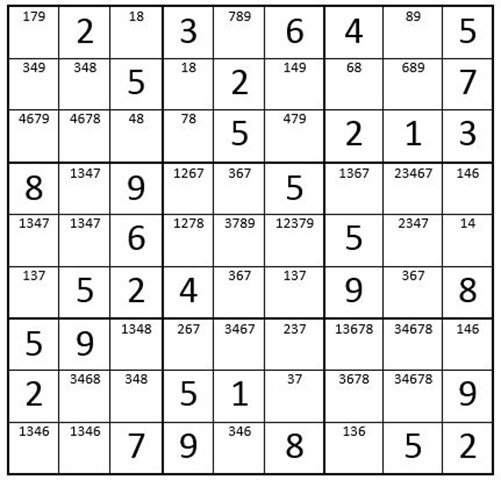
Example 8 with all possible numbers displayed |
|
Conclusion of Part 1 of a 6 Part Series: The next article in this series will cover the twists and turns of Pairs, Triplets and Quads.
For those readers who wish to purchase Dan’s book, it is available at three locations online, (djlsuniverse.com, amazon.com and ebay.com) and at the Porch and Paddle, 236 James Street, Clayton, NY. 315-686-3148.
Purchase of a book includes a 50 page blank grid pad, 33 black and two green tokens to assist with Step 6.
|
By Dan LeKander, Wellesley Island, NY
Dan LeKander and his wife, Peggy, have been seasonal residents of Fineview on Wellesley Island since 1983. In addition to being a Sudoku addict, Dan explores the 1000 Islands to enjoy the wildlife, beauty, and of course, Catch-and Release bass fishing.
[See Jessy Kahn’s Book Review, “3 Advanced Sudoku Techniques…” by Dan LeKander, June issue of TI Life.]