Editor’s note: Do you tackle a Sudoku on your cottage veranda, sailboat cockpit, or at a campsite? TI Life is taking full advantage of Dan LeKander, from Wellesley Island, who is a Sudoku expert and author of “3 Advanced Sudoku Techniques – That Will Change Your Game Forever!” This is Part 3 of 6 Parts of his 8 Step Approach.
|
After completing the July 2015 puzzle preparation by filling in all obvious answers and indicating the options at the top of the unsolved cells, you are ready to use techniques to arrive at a solution to the Sudoku puzzle. The August issue of TI Life explains Dan’s step 1, which involves identifying Pairs, Triplets, and Quads.
STEP 2 …TURBOS & INTERACTIONS
These two techniques can be accomplished at the same time, as you search for them starting in box 1 and then 2-9. Both techniques are very common and will help you remove options from unsolved cells.
TURBOS … This technique is known by different names. Somehow “Turbo” stuck with me and it is an easy name to remember. Starting with box 1 you look for two (and only two) unsolved cells that contain the same option, such as the number 1.
Another criterion is that the two unsolved cells cannot be in the same row or column.
|
Example 1
|
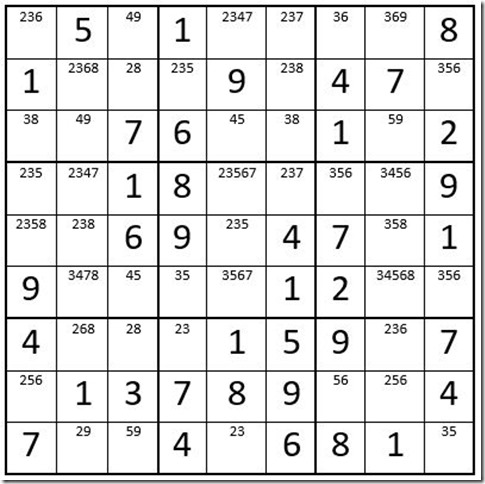
Example 1 actually has three Turbos. Going through boxes 1-9; in box 2 you find that the option “5” exists in just two cells C4R2 (column 4, row 2) and C5R3, these two cells are not in the same row or column. We will call these cells the “driver cells”. For demonstration purposes we will highlight those two driver cells in yellow in Example 2 below.
Example 2
|
The next step is to look at one of the driver cells (in this case we will look at C5R3) to see if there is only one other unsolved cell, in a row or column outside of box 2.
There are three other cells in column 5 that contain a “5” as an option, so that will not work. Look at Row 3. Only one other cell in row 3 has a “5” as an option;. C8R3, so we highlight that cell in orange, as above.
Now go to C4R2 to see if there is one and only one unsolved cell in column 4 that has “5” as an option. Yes; C4R6, so we highlight that cell in orange. Where the two orange cells intersect on the puzzle grid is cell C8R6, which we have highlighted in green.
Here is the theory. If C4R2 = 5, then C5R3 is not a 5; therefore C8R3 = 5, and then the green cell is not a 5.
Switch it around. If C5R3 is a 5, then C4R2 is not a 5; therefore C4R6 = 5, and then the green cell is not a 5.
So regardless of which yellow cell equals 5, the green cell is not a 5 and the “5” can be eliminated from the green cell.
You only need to prove this to yourself once. From that point on it is best not to question yourself, each time you find a Turbo. Trust me, it works every time. Just remember the rules!
1. Find two unsolved cells (and only two cells) in a box, with the same option number(s), which are not in the same row or column. These two cells become the driver cells.
2. Pick one of the driver cells to see if there is just one other unsolved cell in the same row with the same option number. If yes, then look at the column for the other driver cell, to see if there is just one other unsolved cell in the same column, and not the same box, with the same option number.
3. If the unsolved cell, where these two cells intercept, contains the same option number, you may eliminate that option number from that cell.
Just remember; when you find two driver cells, you need to look at a column for the first driver cell and a row for the other. Then look at the row for the first driver cell, and then the column for the other.
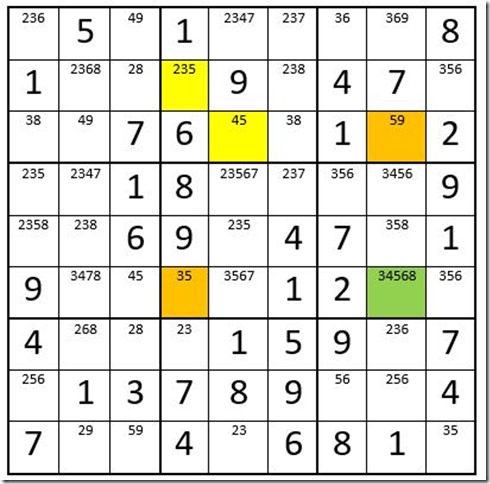
We continue with the same puzzle (with the 5 removed from cell C8R6.)
Example 3
|
Here again in box 7 the driver cells are highlighted in yellow. There is only one other cell in column one that has a 6, and there is only one other cell in row seven that has a 6. Where those two cells intersect is the green cell, and you can remove the “6” in that cell as an option.
Please note that removing the 6 from the green cell sets up another possible Turbo in box 3 with the option 6. This is unsuccessful because the intersected cell is already solved as you look at the driver cells in each direction.
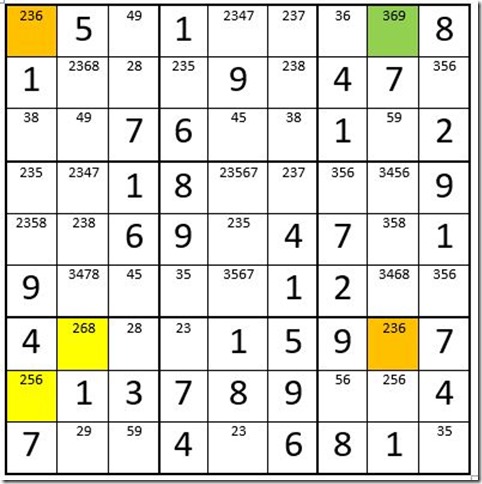
We continue with the same puzzle (with the 6 removed from cell C8R1).
Example 4
|
Here again in box 8 the driver cells are highlighted in yellow. There is only one other cell in column four that has a 2, and there is only one other cell in row nine that has a 2. Where those two cells intersect is the green cell, and you can remove the “2” in that cell as an option.
We will examine a different puzzle for a possible Turbo.
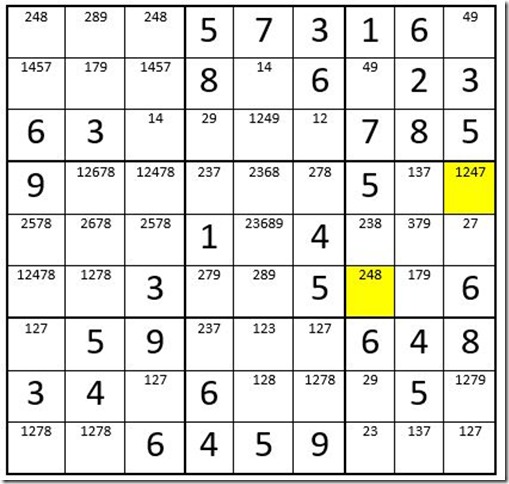
Example 5
|
Please note the two driver cells highlighted in yellow are the only two unsolved cells in box 6 that have a 4 as an option. Applying the Turbo Technique you find that C1R1 cannot be a 4. If you go the reverse directions for the driver cells, you find that C3R2 cannot be a 4. If you go the reverse directions for the driver cells you find that C3R2 cannot be a 4. It is extremely rare for two driver cells to work in “both directions”.
With some practice you will find Turbos are easy to detect and a tremendous source of fun.
INTERACTION … This technique also involves looking at box 1 through 9. We will be looking for ways that a particular number presents itself, in relation to other cells in that box, column, or row.
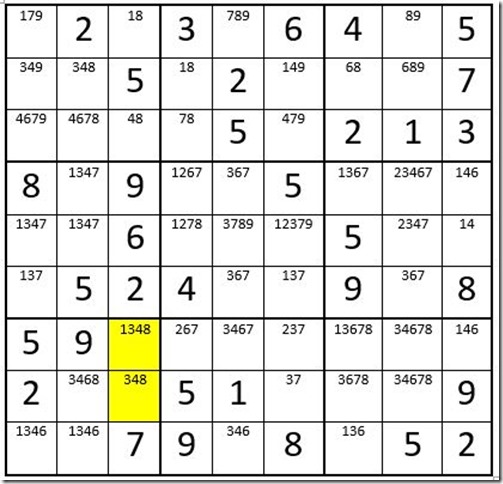
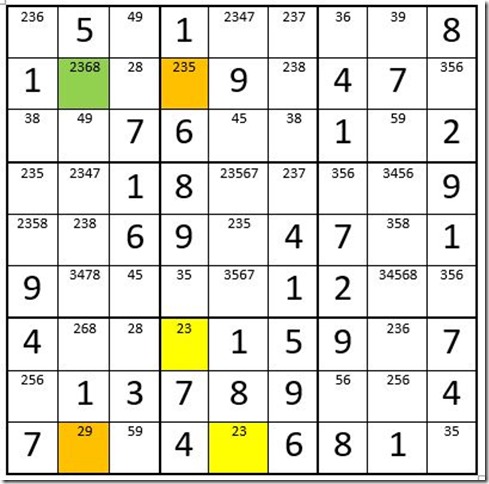
Example 6
|
In example 6, please examine the two cells highlighted in yellow. They are the only two cells in column 3 that contain the option “3”. Therefore one of those two cells must be a 3. If that is true, then no other cells in box 7 can contain a 3 as an option. You may then eliminate the 3 as an option in cells C1R9, C2R8 and C2R9! In this example the eliminated options are in the same box as the yellow cells.
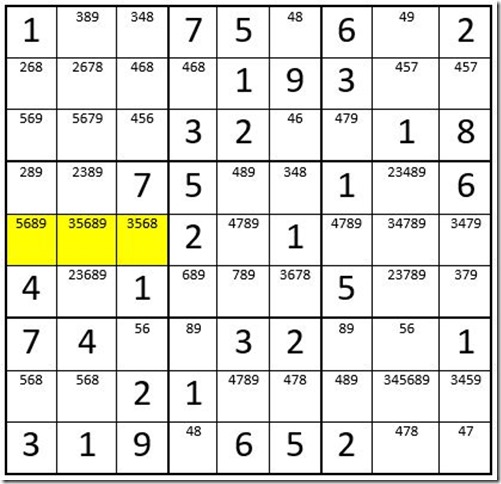
Example 7
|
In example 7, we first find an Interaction similar to Example 6. The yellow highlighted cells are the only cells in row 5 that have a “6” as an option. Therefore the 6 can be eliminated in cell C2R6! So are we finished finding Interactions in this puzzle?
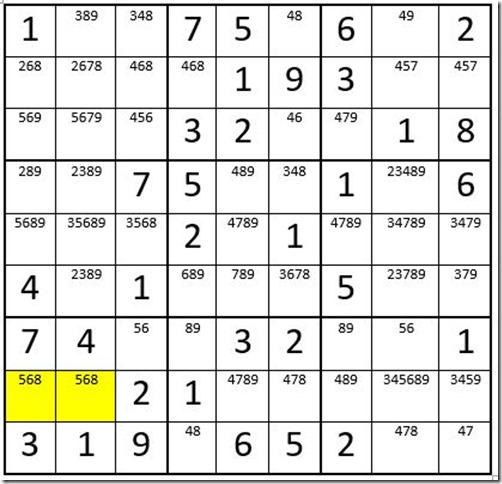
Example 8
|
Example 8 is the same grid as in Example 7, except the 6 has been eliminated as an option, from cell C2R6 and two cells in box 7 are highlighted.
The yellow highlighted cells are the only cells in box 7 that contain an 8. One of these cells must be an 8. Therefore the option “8” may be eliminated from the other unsolved cells in row 8! In this instance, the option 8 is eliminated from four cells! Please note that the eliminated options are not in the same box as the yellow cells.
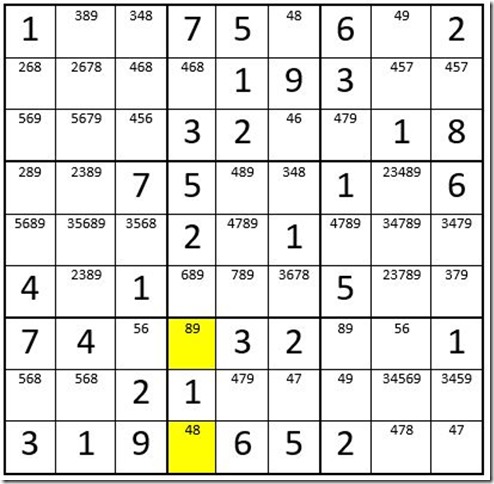
Example 9
|
Example 9 is the same grid as in Example 8, except the 8 has been eliminated as an option from the other cells in row 8, and two cells in box 8 are highlighted.
Ok, so what just happened? The Interaction in Example 8 creates another Interaction; the 8 can be eliminated from C4R2 and C4R6! Also, the Interaction in Example 8 creates a triplet in row 7 (cells C5R8, C6R8 and C7R8 create a “479”; the 4, 7, and 9 can be removed as an option from the other cells in row 8. Then nice things start to happen, like C6R1 = 8.
Conclusion
Note, in Dan’s step 2 you start with box 1 and review numbers 1 through 9, searching for Turbos and Interactions. You then search boxes 2 through 9 in a similar fashion. You have now witnessed how Turbos and Interactions can eliminate many options from a puzzle. With a little practice you can master these techniques!
Ok, now it is your turn.
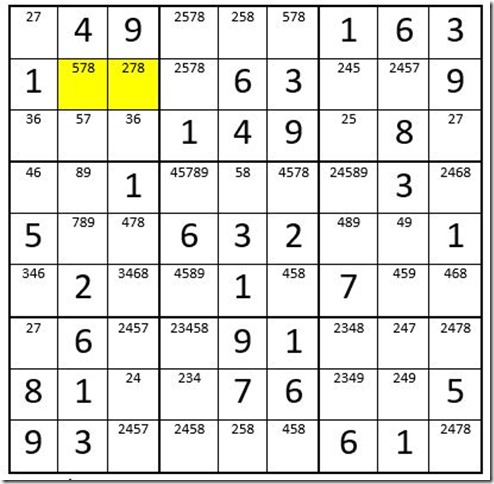
Example 10
|
See if you can find at least seven Interactions in Example 10. (By the way, this might be a record number of Interactions in one puzzle.) Two unsolved cells in box 1 are highlighted in yellow to give you a JUMP start.
Answers to Example 10
- C2R2 and C3R2 eliminate an 8 from C4R2
- C4R1, C5R1 and C6R1 eliminate a 5 from C4R2
- C7R3 and C9R3 eliminate a 2 from C7R2 and C8R2
- C1R4 and C1R6 eliminate a 4 from C3R5 and C3R6
- C7R5 and C8R5 eliminate a 4 from C7R4, C8R6, C9R4 and C9R6
- C8R7 and C8R8 eliminate a 2 from C7R7, C7R8, C9R7 and C9R9
- C9R7 and C9R9 eliminate a 4 from C7R7, C7R8, C8R7 and C8R8
|
Conclusion of Part 3 of a 6 Part Series:
The next article will cover the techniques “Gordonian Rectangles, Polygons, & Variations of Both”.
For those readers who wish to purchase Dan’s book, it is available at three locations online: (djlsuniverse.com, amazon.com and ebay.com).
Purchase of a book includes a 50 page blank grid pad, 33 black and two green tokens, to assist with Step 6.…
|
By Dan LeKander, Wellesley Island, NY
Dan LeKander and his wife, Peggy, have been seasonal residents of Fineview on Wellesley Island since 1983. In addition to being a Sudoku addict, Dan explores the 1000 Islands to enjoy the wildlife, beauty, and of course, Catch-and Release bass fishing.
[See Jessy Kahn’s Book Review, “3 Advanced Sudoku Techniques…” by Dan LeKander, June issue of TI Life.
]