Our theme this month is “UNLEASH THE POWER OF STEP 6”! We will take a very close look at using Step 6 to your advantage with Puzzle # 24.
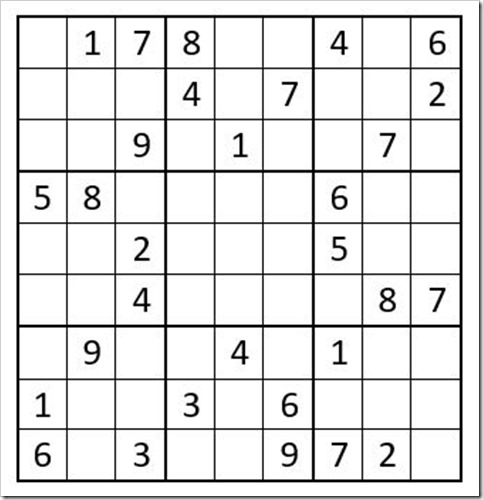
Puzzle # 24
|
First, we will revisit the approach, as discussed in my first 6 TI Life articles.
| |
DAN’S 8 STEP APPROACH TO SOLVING ALL SUDOKU PUZZLES
Once you have completed the puzzle, to the extent that you have filled in all obvious answers and have written all potential options across the top of the unsolved cells (PUZZLE PREPARATION), Dan recommends the following steps to complete the puzzle.
See TI Life Puzzle Preparation:
Step 1: Sudoku Pairs, Triplets and Quads – September, 2015
Step 2: Turbos & Interaction – October, 2015
Step 3: Sudoku Gordonian Rectangles and Polygons – November, 2015
Step 4: XY-Wings & XYZ Wings – December, 2015
Step 5: X-Wings – January, 2016
________________
Step 6: DAN’S YES/NO CHALLENGE
Step 7: DAN’S CLOSE RELATIONSHIP CHALLENGE
Step 8: AN EXPANSION OF STEP 7
Steps 1-5 are relatively common techniques and are explained in the TI LIFE articles per above. Steps 6-8 are covered in detail, in Dan’s book.
Also see Sudoku Puzzle Challenge… February 2016, Sudoku Puzzle Challenge–March 2016, Sudoku Puzzle Challenge–April 2016, May 2016, June 2016, July 2016, August 2016, September 2016, October 2016, November 2016, December 2016, January 2017, February 2017 and March 2017.
|
As a reminder, the basic rules of Sudoku are that the numbers 1-9 cannot be repeated in a row, column, or box, and there can only be one solution to the puzzle.
PUZZLE PREPARATION
First, we will complete the 4 Steps of Puzzle Preparation:
- Fill in the obvious answers
- Fill in the not-so-obvious answers
- Mark unsolved cells with options that cannot exist in those cells
- Fill in the potential options for the unsolved cells
OBVIOUS ANSWERS … Start with the 1’s to see if there are any obvious 1-choice answers. Then navigate your way through the 2’s to 9’s.
The first obvious answer is C3R4 (cell in column 3, row 4) =1. C4R9=1, C8R2=1, C9R5=1, C6R6=1 and that concludes the 1’s. Then C7R6=2, C8R7=6 & C9R7=3.
NOT SO OBVIOUS ANSWERS … In box 4 (grid of 9 cells in middle left) a 6 can exist only in C2R5 or C2R6 because of the 6 in C1R9; therefore, the only unsolved cell in box 1 that can be a 6 is C3R2. C3R2=6. Then C4R3=6.
In box 7 a 4 can exist only in C2R8 or C2R9; therefore, a 4 cannot exist in C2R2 or C2R3; therefore, the only unsolved cell in box 1 that can be a 4 is C1R3. C1R3=4. Then C1R2=8.
In box 7 a 2 or 7 can only exist in C1R7 or C2R8, so mark the top of those 2 cells as “27” as per Example #24.1 below. Also in column 3 a 5 or 8 can only exist in C3R7 and C3R8. Mark those as “58”. You can then see that C2R9 must be a 4. C2R9=4.
Now your grid should look like Example #24.1 below:
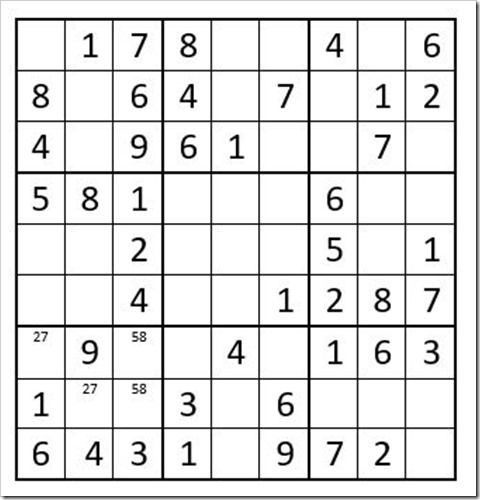
Example # 24.1
|
NUMBERS IN UNSOLVED CELLS THAT CANNOT EXIST:
In box 6, a 3 can only exist in C8R4 or C8R5 because of the 3 in C9R7; therefore, a 3 cannot exist in C8R1. Indicate this by placing a small “3” in the bottom of C8R1. This will be your reminder later, to not include a 3 as an option for C8R1.
In box 4, a 7 can exist only in C1R5 or C2R5; therefore, a 7 cannot exist in C5R5 or C6R5 (we already know that a 7 cannot exist in C8R5).
In box 2, a 9 can only exist in C5R1 or C5R2; therefore, a 9 cannot exist in C5R4, C5R5 or C5R6.
Now your grid should look like Example #24.2 below:
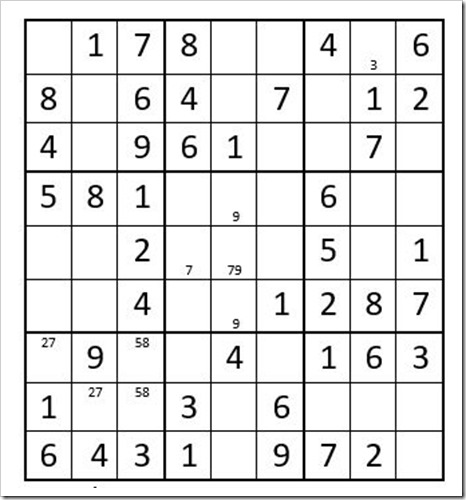
Example # 24.2
|
FILL IN THE OPTIONS FOR THE UNSOLVED CELLS:
When we fill in the options for C4R5 we see that a 9 is the only choice. C4R5=9. Then looking at column 4 we see that the only choice for C4R6 is a 5, because of the 2 & 7 already existing in row 6. C4R6=5. Then looking at C1R6, we see that it must be a 9. C1R6=9.
While filling in the options, we see 3 obvious pairs, which you should process as soon as you see them rather than waiting for Step 1.
1. Now the options in column 4, for C4R4 & C4R6, are “27”. That leaves C1R7 & C4R7 with an obvious pair “27”. Removing the 2 from C6R7 leaves that cell with options “58”.
2. In column 9 we find that C9R3 & C9R9 have options “58”; therefore eliminate the 5 & 8 from C9R8.
3. In box 8, C5R9 & C6R7 have options “58”; therefore, eliminate the 5 & 8 from C5R8.
Please note that we have accomplished significant progress with this puzzle, in the Puzzle Preparation phase. Now your grid should look like Example #24.3 below:
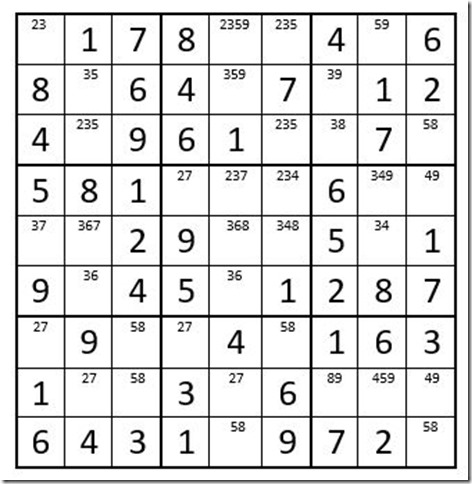
Example # 24.3
|
STEPS 1-8:
STEP 2: INTERACTION & TURBO’S … C1R7 & C2R8 form a Turbo with C1R1 & C5R8 to eliminate the 2 from C5R1. The results set up a pair of Step 1 opportunities …
STEP 1: PAIRS, TRIPLETS & QUADS
- C5R4 & C5R8 are the only two cells in column 5 that can contain a 2 & 7, eliminating the 3 in C5R4.
- C4R4 & C5R4 form an obvious pair, 2 & 7, eliminating the 2 from C6R4
There are no other Step 1-5’s. See Example #24.4 below:
STEP 6: DAN’S YES-NO CHALLENGE
There are 3 circumstances that establish the potential for a Step 6 exercise:
1. Look for just 2 unsolved cells in a box that contains the same option, whereas these 2 cells are not in the same row or column. An example is C8R1 & C9R3. Each of these 2 cells contain a 5 and are not in the same row or column.
2. Look for just 2 unsolved cells in a column that contains the same option, whereas these 2 cells are not in the same box. An example is C1R1 & C1R7. Each of these 2 cells contain a 2 and are not in the same box.
3. Look for just 2 unsolved cells in a row that contain the same option, whereas these 2 cells are not in the same box. An example is C5R1 & C8R1. Each of these 2 cells contain a 9 and are not in the same box.
Our first potential for a Step 6 that will be successful are cells C8R1 & C9R3. One of these 2 cells must be a 5. We will first assume C8R1 is a 5 and determine which cells cannot be a 5. Then we will assume C9R3 is a 5 and determine which cells cannot be a 5. If a cell cannot be a 5 regardless of which cell in box 3 is a 5, then that 5 can be eliminated from that cell. So, we will start with the assumption that C8R1=5 and indicate this by placing an upper case “Y”, for “yes”, in C8R1, as per Example #24.4 below. If C8R1 is a yes (a 5), then C5R1 & C6R1 are not a 5, so we will mark them with an upper case “N” for “no”. Next we will assume C9R3=5 and mark it with a lower case “y” to not confuse it with the upper case Y and N’s. If C9R3 is a 5, then C9R9 is not a 5, so we will mark it with a “n”. If C9R9 is not a 5, then C5R9 is a 5, and we will mark it with a “y”. If C5R9 is a 5, then C5R1 is not a 5, so we will mark it with a “n”. So C5R1 has a N,n designation and is not a 5, regardless of which cell in box 3 is a 5, so you can eliminate the 5 as an option from C5R1.
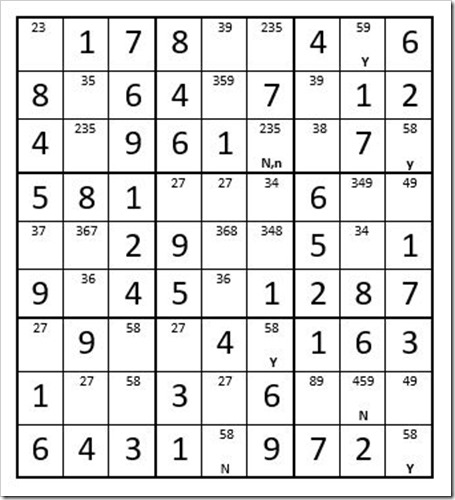
Example # 24.4
|
In Example #24.5 below, the 5 has been removed from C5R1.
Now let’s play this game again, going the opposite direction, with the two “starter cells” C8R1 & C9R3. Follow the yes’s and no’s. C6R3 ends up with a “N,n”, so the 5 can be eliminated, as an option from C6R3.

Example # 24.5
|
Well that exercise did not allow us to solve the puzzle. So let’s look for another Step 6, exercise in Example #24.6 below. We will choose two cells in column 1 that have 3 as an option, which are C1R1 & C1R5, our “driver cells”. Starting out we assume C1R1 is a 3 and mark it with a Y, then C5R1 & C6R1 are not a 3, and we mark them with a N.
Next, we assume C1R5 is a 3 and mark it with a y. Then C5R5, C6R5 & C8R5 are not a 3 and we will mark them with a n. In box 6 if C8R5 is not a 3, then C8R4 has to be a 3. If that is the case, then C5R4 & C6R4 are not a 3. As we examine box 5 we see that the only cell that can be now be a 3 is C5R6 so we will mark it with a y. Therefore, C5R1 cannot be a 3, and we will mark it with a N,n and that brings us to a conclusion that C5R1 is not a 3, eliminating the 3 as an option from C5R1. That leaves C5R1 with a 9 as its only option. C5R1=9.
|

Example # 24.6
|
From this point the puzzle is “unlocked” and is easily solved, giving us Example #24.7 below, as the conclusion:
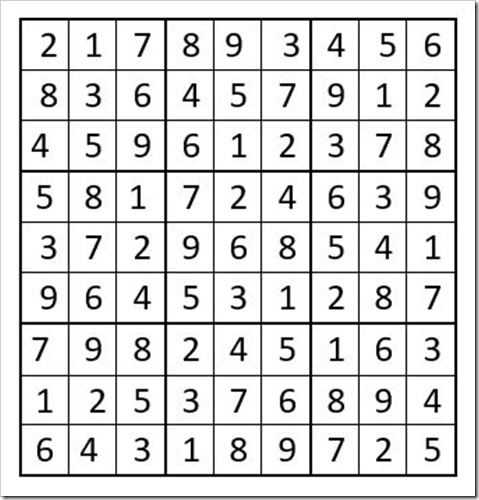
Example # 24.7
|
You now have improved tools to employ Step 6. Some puzzles will yield no successful Step 6’s. Other puzzles may yield multiple successful Step 6’s.
Thank you for your interest. May the gentle winds of Sudoku be at your back.
Editor’s note:
(Photo above… Sudoku is for everyone… you’re never too young to start!)
Do you tackle a Sudoku on your cottage veranda, sailboat cockpit, or at a campsite? TI Life is taking full advantage of Dan LeKander, from Wellesley Island, who is a Sudoku expert and author of “3 Advanced Sudoku Techniques – That Will Change Your Game Forever!”
In January 2016, we published a final article in his original series – but many of us enjoy using “Dan’s Steps,” so when he asked if we would like a puzzle to solve every month … this editor said an enthusiastic… Yes, please!
I suggest you try this relatively difficult puzzle and that you also purchase Dan’s book, “3 Advanced Sudoku Techniques, That Will Change Your Game Forever!”
Most importantly, I ask that you leave comments on any part of his series and throughout the year. Remember when your teacher said – no such thing as a silly question – as we can all learn together.
Dan’s book is available online, amazon.com and on ebay.com.
Purchase of a book includes a 50-page blank grid pad, 33 black and two green tokens, to assist with Step 6.…
Now, with the new year well underway, I want to say THANKS Dan and THANKS to his better half, Peggy LeKander, who helps make sure the article is correct and reads well. What a team!
|
Dan LeKander
Dan LeKander and his wife, Peggy, have been seasonal residents of Fineview, on Wellesley Island, NY, since 1983. In addition to being a Sudoku addict, Dan explores the 1000 Islands to enjoy the wildlife, beauty and of course, Catch-and Release bass fishing.
[See Jessy Kahn’s Book Review, “3 Advanced Sudoku Techniques…” by Dan LeKander, June issue of TI Life.]
Do you have suggestions for future articles or do you want any Step 1-8 techniques explained further? You can post on this article or contact me directly at djlsuniverse@yahoo.com.