Being November, with Thanksgiving around the corner, it is a good time to be thankful for Sudoku. It can be a fun lifetime hobby, with the added benefit of keeping your mind sharp!
On my mind, and perhaps on yours, is enjoying a great turkey dinner. This year had to be a banner year for turkey sightings at the River. In September and October they became very brave and often you needed to stop your car, as they slowly made their way over the highways!
A reader recently asked why I choose difficult puzzles. Newspapers and Sudoku puzzle books are full of easy puzzles, which you may enjoy solving. As your expertise expands you may find solving the truly difficult puzzles brings you quite a different form of satisfaction. I solve about 15 “difficult” puzzles to find one puzzle that requires advanced techniques. These are the puzzles that I feature. Please give this difficult puzzle your best shot before following my lead.
|
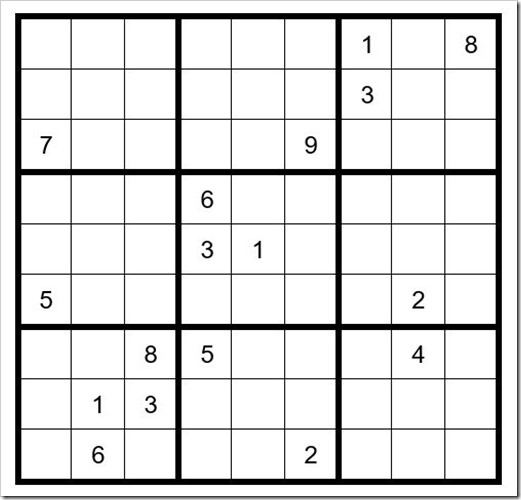
PUZZLE #46
|
DAN’S 8-STEP APPROACH TO SOLVING ALL SUDOKU PUZZLES
Once you have completed the puzzle, to the extent that you have filled-in all obvious answers and have written all potential options across the top of the unsolved cells (PUZZLE PREPARATION), Dan recommends the following Steps to complete the puzzle.
See TI Life Puzzle Preparation:
Step 1: Sudoku Pairs, Triplets and Quads – September 2015
Step 2: Turbos & Interaction – October 2015
Step 3: Sudoku Gordonian Rectangles and Polygons – November 2015
Step 4: XY-Wings & XYZ Wings – December 2015
Step 5: X-Wings – January 2016
________________
Step 6: DAN’S YES/NO CHALLENGE
Step 7: DAN’S CLOSE RELATIONSHIP CHALLENGE
Step 8: AN EXPANSION OF STEP 7
Steps 1-5 are relatively common techniques and are explained in the TI LIFE articles above. Steps 6-8 are covered in detail, in Dan’s book.
Also, see Sudoku Puzzle Challenge… February 2016, March 2016, April 2016, May 2016, June 2016, July 2016, August 2016, September 2016, October 2016, November 2016, December 2016, January 2017, February 2017, March 2017 , April 2017, May 2017, June 2017, July 2017, August 2017, September 2017, October 2017 , November 2017 , December 2017, January 2018, February 2018, March 2018, April 2018. May 2018, June 2018, July 2018, August 2018, September 2018 and October 2018.
As a reminder, the basic rules of Sudoku are that the numbers 1-9 must be contained and cannot be repeated in a row, column, or box, and there can only be one solution to the puzzle.
|
PUZZLE PREPARATION
Prior to utilizing ,first complete the 4 Steps of Puzzle Preparation…
- FILL IN OBVIOUS ANSWERS
- FILL IN NOT-SO-OBVIOUS ANSWERS
- MARK UNSOLVED CELLS WITH OPTIONS THAT CANNOT EXIST IN THOSE CELLS
- FILL IN THE OPTIONS FOR THE UNSOLVED CELLS
OBVIOUS ANSWERS …
Start with the 1’s to see if there are any obvious 1-choice answers. Then navigate the 2’s through 9’s.
The first obvious answer is C5R4=2 (cell in column 5, row 4). C3R9=5. C2R7=7.
Now your grid should look like Example #46.1 below:
|
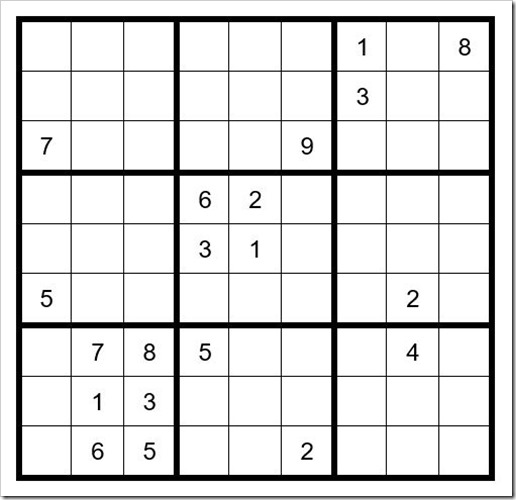
Example #46.1
|
NOT-SO-OBVIOUS ANSWERS … There are none.
MARK UNSOLVED CELLS WITH OPTIONS THAT CANNOT EXIST IN THOSE CELLS …
In box 5 (center grid of 3 x 3 cells) a 5 can exist only in C6R4 or C6R5; therefore, a 5 cannot exist as an option in C6R1 or C6R2. Pencil a small 5 in the bottom of those 2 cells to indicate they cannot be a 5.
In box 5 a 9 can only exist in C4R6 of C5R6; therefore, a 9 cannot exist in C2R6, C3R6, C7R6 or C9R6.
In box 7 the options for cells C1R7, C1R8 & C1R9 can only be 2, 4, & 9; therefore, the other cells in column 1 cannot be a 2, 4 or 9.
Now your grid should look like Example #46.2 below:
|
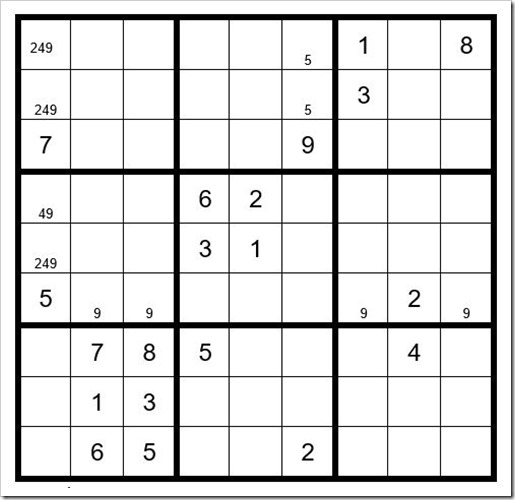
Example #46.2
|
FILL IN THE OPTIONS FOR THE UNSOLVED CELLS …
Once you fill in the options for the unsolved cells, your grid should look like Example #46.3 below:
|
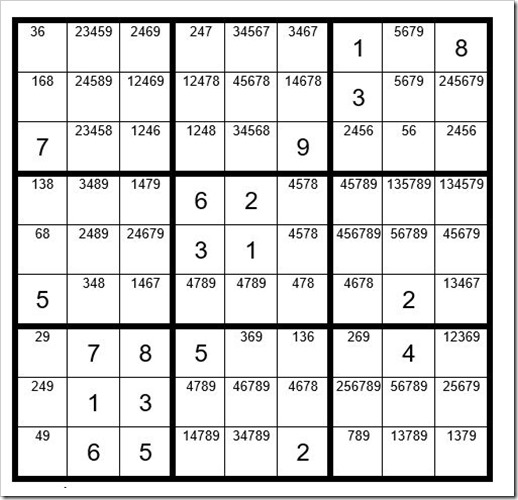
Example #46.3
|
STEPS 1-8
We will begin with Step 1, identifying Pairs, Triplets, Quads & Quints. We will search each row, column and box. Can you spot any Step 1 clues in Example #46.3 above?
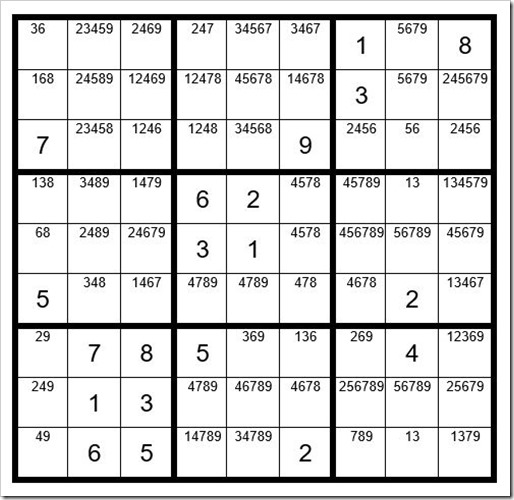
Take a closer look at column 8. Can you spot a Step 1 clue?
Column 8 has a hidden pair & a quint. Take your choice as the result is the same. We see that C8R4 & C8R9 are the only two cells in column 8 that contain the options 1 & 3. Therefore, all other options for those two cells can be eliminated. Now your grid should look like Example #46.4 below:
|
Example #46.4
|
There are no other Step 1-5 clues. We will now move to Step 6: Dan’s Yes-No Challenge.
There are 3 circumstances that establish the potential for a Step 6 exercise:
- Look for just 2 unsolved cells in a box that contain the same option where these 2 cells are not in the same row or column.
- Look for just 2 unsolved cells in a column that contain the same option where these 2 cells are not in the same box.
- Look for just 2 unsolved cells in a row that contain the same option where these 2 cells are not in the same box.
We will start by searching the 1’s to see if there is a potential Step 6 clue, and then navigate through the 2-9’s.
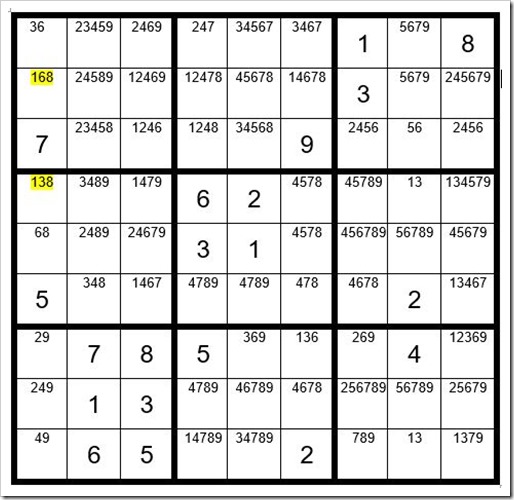
In column 1 we find just 2 unsolved cells that contain the option 1 … C1R2 & C1R4. These cells are not in the same box, thereby qualifying as a candidate for a Step 6 exercise. The options in these cells are highlighted in yellow in Example #46.5 below:
|
Example #46.5
|
Do you agree that one of these two yellow cells in column 1 must be a 1? We will consider them as “driver cells” which “drive” the exercise.
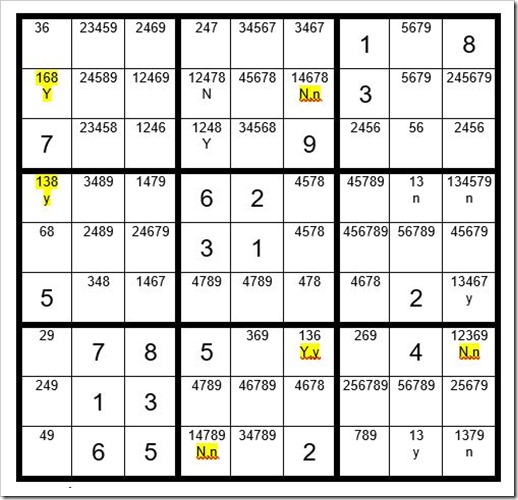
Here is the logic. We will perform two exercises. First, we will assume C1R2 is the 1 and see which other cells cannot be a 1. Then we will assume C1R4 is the 1 and see which other cells cannot be a 1.
We will mark C1R2 with a “Y” and mark C1R4 with a lower case “y” to keep track of the exercise as per Example #46.6 below.
|
Example #46.6
|
We will start by assuming C1R2=1. Then, as marked above, C7R3 and C8R3 are not a 1 (marked with a “N”). Now the only cell in box 2 that can be a 1 is C4R3, so we will mark it as a “Y”. Then, C4R9=N. C6R7=Y. C9R7=N.
Now we will assume C1R4=1 (y for yes). Then, C8R4=n & C9R4=n. C9R6=y. C9R7=n & C9R9=n. C8R9=y. C4R9=n. C6R7=y. C6R2=n.
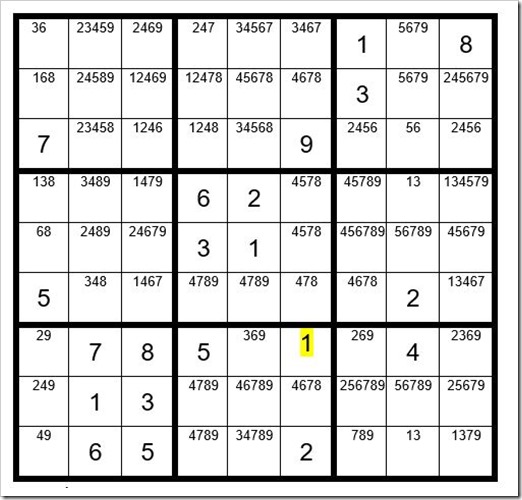
We now see in Example #46.6 above that C4R9, C6R2 & C9R7 have a “N,n” designation. What does that mean? Since we know one of the two yellow highlighted cells in column 1 must be a 1, the N,n cells cannot be a 1 regardless of which starter cell is a 1. Likewise, C6R7 has a Y,y designation, meaning it is a 1 regardless of which starter cell is a 1.
Now your grid should look like Example #46.7 below:
|
Example #46.7
|
It now follows that C6R1=3, C1R1=6, C1R5=8, C1R2=1, C1R4=3, C2R6=4, C2R4=9, C2R5=2, C2R1=5, C2R2=8, C2R3=3. From this point the puzzle is easily solved.
Your final grid should now look like Example #46.8 below:
|
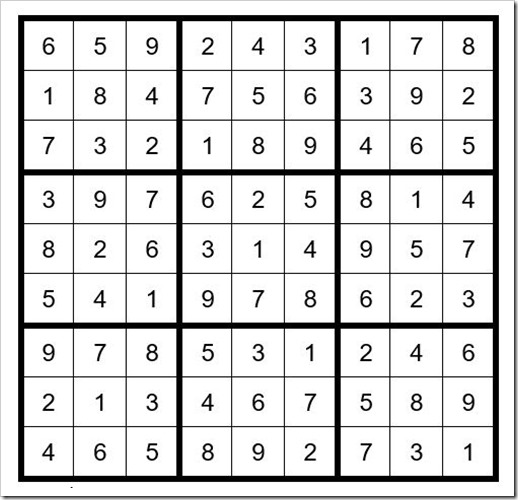
Example #46.8
|
May the gentle winds of Sudoku be at your back.
Dan LeKander
Editor’s note:
Now the cold weather is here, we ask the question :Do you tackle a Sudoku beside your fireplace, on the bus going to work or anywhere you have the chance? Write and tell us where? OK. (I start mine with a cup of coffee and CBC Radio Classical music playing… but not on the island.)
TI Life is taking full advantage of Dan LeKander, from Wellesley Island, who is a Sudoku expert and author of “3 Advanced Sudoku Techniques – That Will Change Your Game Forever!”
In January 2016, we published a final article in his series – but many of us enjoy using “Dan’s Steps,” so when he asked if we would like a puzzle to solve every month … this editor said an enthusiastic… Yes, please! Now we are several years later and on Puzzle #46!
I suggest you purchase Dan’s book, “3 Advanced Sudoku Techniques, That Will Change Your Game Forever!”
Dan’s book is available online, amazon.com and on ebay.com.
Purchase of a book includes a 50-page blank grid pad, 33 black and two green tokens, to assist with Step 6.…
Most importantly, I ask that you leave comments on any part of his series and throughout the year. Remember when your teacher said – no such thing as a silly question – as we can all learn together.
As always, I want to thank Dan…and his proofreader… Peggy! I am hoping you will enjoy our Sudoku and at the same time join me in thanking Dan - I have a hard time doing the puzzles – let alone creating them! Bravo.
|