Please enjoy the journey as we tackle an extreme Sudoku puzzle!
Puzzle #23 will require advanced techniques. In the step-by-step explanation that follows you will see that we simply use Dan’s 8-Step Approach, which works every time! Whether you decide to solve the puzzle yourself or follow along, you may want to print Puzzle #23. This will be a great chance to hone your Sudoku skills.
First, we will revisit the approach as discussed in my first six TI Life articles.
| |
DAN’S 8 STEP APPROACH TO SOLVING ALL SUDOKU PUZZLES
Once you have completed the puzzle, to the extent that you have filled in all obvious answers and have written all potential options across the top of the unsolved cells (PUZZLE PREPARATION), Dan recommends the following steps to complete the puzzle.
See TI Life Puzzle Preparation:
Step 1: Sudoku Pairs, Triplets and Quads – September, 2015
Step 2: Turbos & Interaction – October, 2015
Step 3: Sudoku Gordonian Rectangles and Polygons – November, 2015
Step 4: XY-Wings & XYZ Wings – December, 2015
Step 5: X-Wings – January, 2016
________________
Step 6: DAN’S YES/NO CHALLENGE
Step 7: DAN’S CLOSE RELATIONSHIP CHALLENGE
Step 8: AN EXPANSION OF STEP 7
Steps 1-5 are relatively common techniques and are explained in the TI LIFE articles per above. Steps 6-8 are covered in detail, in Dan’s book.
Also see Sudoku Puzzle Challenge… February 2016, Sudoku Puzzle Challenge–March 2016, Sudoku Puzzle Challenge–April 2016, May 2016, June 2016, July 2016, August 2016, September 2016, October 2016, November 2016, December 2016, January 2017 and February 2017.
|
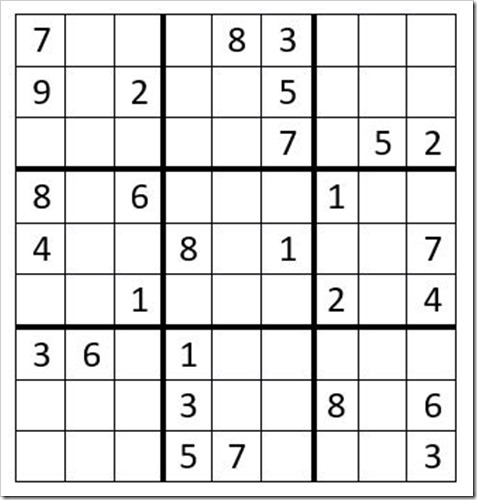
Puzzle # 23
|
As a reminder, the basic rules of Sudoku are that the numbers 1-9 cannot be repeated in a row, column, or box, and there can only be one solution to a puzzle.
PUZZLE PREPARATION
First, we will complete the 4 steps of Puzzle Preparation …
1. Fill in the obvious answers
2. Fill in the not-so-obvious answers
3. Mark the unsolved cells with the options that cannot exist in those cells
4. Fill in the potential options for the unsolved cells
OBVIOUS ANSWERS … Start with the 1’s to see if there are any obvious 1-choice answers (a 1-choice answer means there is only one number of 1-9 that will work in that cell or there is only one choice for a number in a particular cell in a box, column, or row). Then navigate your way through the 2’s to 9’s.
The first obvious answer is C4R1 (cell in column 4, row 1) = 2, then C1R3=6, C6R9=6, C8R6=8, C9R2=8, and C6R7=8.
NOT SO OBVIOUS ANSWERS … The only cell in column 9 that can be a 1 is C9R1.
In column 1 the choices for C1R6 are 1,2 & 5. There exists a 1 & 2 in row 6, so C1R6=5.
In column 6 the choices for C6R6 are 2,4 & 9. There exists a 2 & 4 in row 6, so C6R6=9.
The only cell in column 4 that can be a 9 is C4R3.
Now your grid should look like Example #23.1 below:
Example #23.1
NUMBERS IN UNSOLVED CELLS THAT CANNOT EXIST …
In box 1, (grid of 9 cells in upper left) a 1 cannot exist in C3R1 or C3R3 because of the 1 in C3R6. Additionally, a 1 cannot exist in C2R1 because of the 1 in C9R1; therefore, a 1 must exist in either C2R2 or C2R3; therefore, a 1 cannot exist in C2R8 or C2R9. We will indicate this by placing a small 1 in the bottom of cells C2R8 & C2R9.
In box 4 (middle left) a 2 must exist in C2R4 or C2R5; therefore a 2 cannot exist in C2R8 or C2R9. You can arrive at the same result by recognizing cells C1R8 & C1R9 must have options 1 & 2, which is an “obvious pair”. Thus the other unsolved cells in box 7 cannot have options 1 & 2.
In box 9 a 5 must exist in C7R7 or C9R7; therefore, a 5 cannot exist in C3R7.
In box 6 a 6 must exist in C7R5 or C8R5; therefore, a 6 cannot exist in C5R5.
In box 2 a 6 must exist in C4R2 or C5R2; therefore, a 6 cannot exist in C7R2 or C8R2.
In box 4 a 7 must exist in C2R4 or C2R6; therefore, a 7 cannot exist in C2R8 (we already know that a 7 cannot exist in C2R9).
Now your grid should look like Example #23.2 below:
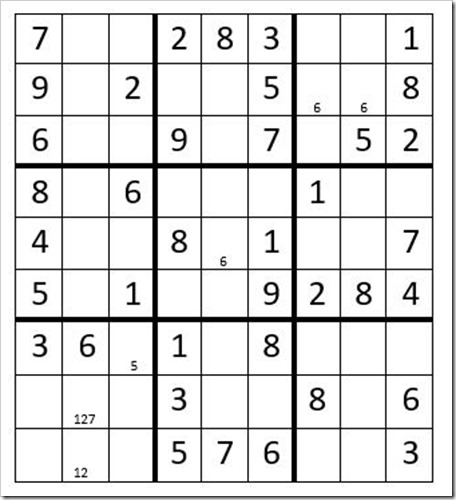
Example # 23.2
|
FILL IN THE OPTIONS FOR THE UNSOLVED CELLS …
Your grid should now look like Example 23.3 below:
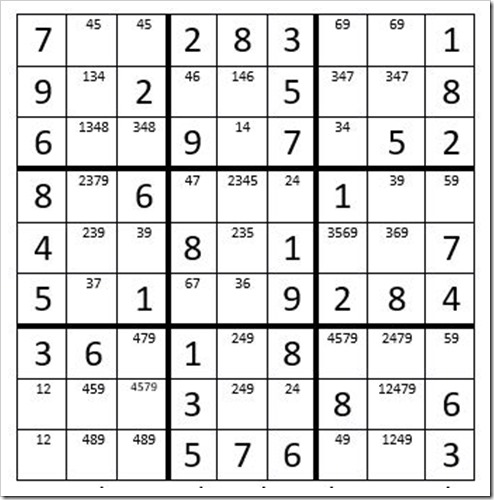
Example # 23.4 Through Puzzle Preparation
|
STEP 1-8
I suggest exploring Steps 1-8 in numerical order with the realization that a successful step might set the stage for returning to an earlier step. For example, a Step 5 X-WING might eliminate an option from a particular cell, which then creates a Step 1 PAIR. When a technique eliminates an option from a cell, ask yourself what effect that has on your grid and mentally scan to see if that sets up a previous technique.
STEP 1: PAIRS, TRIPLETS & QUADS
· C2R1 & C3R1 are an obvious pair 45. Notice above we have already taken into account C7R1 & C8R1 do not contain options 4 & 5. But what about box 1? Yes, we need to eliminate the 4 & 5 from any other unsolved cells in box 1. Remove the 4 from C2R2, C2R3 & C3R3.
· C8R1, C8R4 & C8R5 form a triplet 369. We can eliminate a 3, 6, & 9 from all other cells in column 8. Remove the 3 from C8R2, the 9 from C8R7, C8R8 & C8R9.
· C2R9, C3R9 & C7R9 form a triplet 489. Eliminate the 4 from C8R9.
STEP 3: GORDONIAN RECTANGLES & POLYGONS
· C1R8, C1R9, C8R8 & C8R9 form a Gordonian Rectangle Plus. For a complete explanation please visit the TI Life article referenced (and linked) earlier. However, the short explanation is based on the rule of Sudoku that there can only be one answer to a Sudoku Puzzle. The theory is that if C8R8 had only options 12, there would eventually be two valid solutions to the puzzle. The net result is that C8R8 cannot be a 1 or 2, so we eliminate them as options leaving 4 & 7 as the options for C8R8.
STEP 1: PAIRS, TRIPLETS & QUADS.
· Here is a prime example of needing to revert to an earlier technique as a result of another technique. In Step 3 above we reduced the options for C8R8 to 47. Looking at C8R2 we see that its options are also 47. This is an obvious pair, so we can eliminate the 4 & 7 from any other cell in column 8. Remove the 4 & 7 from C8R7, leaving the only option for that cell a 2. C8R7=2. Then C8R9=1. C1R9=2. C1R8=1. Remove the 2 as an option for C5R7.
STEP 2: INTERACTION & TURBOS
· C7R2 & C7R3 form an Interaction with 3’s, eliminating the 3 from C7R5. (In box 3 the only two cells that contain a 3 are C7R2 & C7R5; therefore, one of these two cells must be a 3. Hence, C7R5 cannot be a 3.
Now your grid should look like Example #23.4:
|

Example # 23.4
|
This completes Steps 1-5, so we will move on to Step 6.
STEP 6: DAN’S YES-NO CHALLENGE
We start by searching boxes starting with the 1’s, then 2’s, etc. looking for Step 6 opportunities. Once we get to the 4’s we find a promising Step 6 with C8R2 & C8R8 in column 8, (highlighted in yellow), as per Example #23.5 below. One of these two cells must be a 4. First we will assume C8R2 is a 4 and indicate in this cell a “Y” for yes. Then we will mark C4R2, C5R2 & C7R2 with an “N”, meaning that if C8R2 is a 4, then C4R2, C5R2 & C7R2 not a 4. In box 2 if those cells are a no, then C5R3 must be a yes. Then C5R4, C5R7 & C5R8 are a no. Now the only cell in box 8 that can be a 4 is C6R8 so we will mark it with a Y. Then C2R8 & C3R8 are a no.
Next we will assume C8R8 is a 4 and mark it with a lower case “y” to differentiate from the “Y” in C8R2. Now follow the results as we apply “y’s” and “n’s” as a result of C8R8 being a 4. C2R8, C3R8, C5R8 & C6R8 are all no (“n”). C5R7 is “y”. C5R2, C5R3 & C5R4 are “n”. Then C4R2 must be a “y”, and then C7R2 must be a “n”.
|
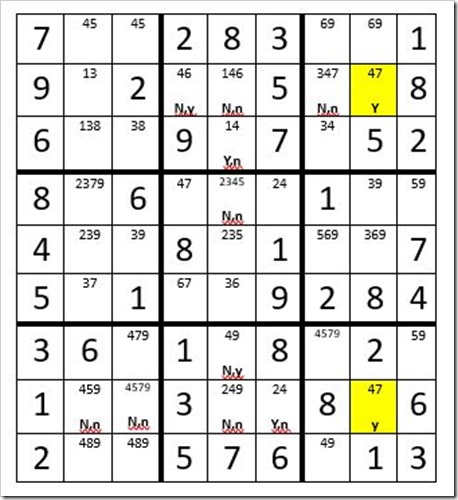
Example # 23.5
|
At this point you might be asking yourself, “What kind of fire drill is this?” Actually, any cell with a “N,n” cannot be a 4! Consider why. We know for sure that one of the two yellow cells is a 4. Pick any “N,n” cell. Let’s look at C7R2. We know that if C8R2 is a 4, then C7R2 is not a 4. If C8R8 is a 4, then C4R2 is not a 4. So regardless of which yellow cell is a 4, C7R2 is not a 4. We know that this same reasoning applies to all other cells with a “N,n”. So now eliminate the 4 from C5R2, C5R4, C7R2, C2R8, C3R8 & C5R8. Now your grid should look like Example #23.6 below:
|
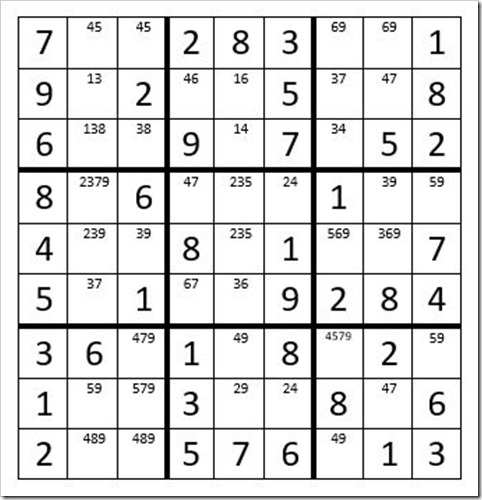
Example # 23.6
|
STEP 7: DAN’S CLOSE RELATIONSHIP CHALLENGE
To begin this technique, we pick any 2-digit unsolved cell. In Example #23.7 below we have chosen C5R8 (highlighted in yellow) with the sequence 2,9 as designated on the 2nd level of that cell. At this point we are not concerned whether C5R8 is a 2 or 9. Instead we are interested in the “relationship” of C5R8 to other unsolved cells in the same box, row & column with a 2 as an option. If C5R8 is a 2, then C5R4 & C5R5, (highlighted in blue), cannot be a 2. We indicate this by placing an “N2” in the second level of the blue cells. The second number of the 2,9 in C5R8 is a 9. We will “track” the 9 through the puzzle to see which of the 2 blue cells is not a 2, for there can only be 1 cell in column 5 that is a 2. If the tracking goes far enough we will be successful. Plus as we perform this technique we may discover other benefits. Now we track the 9 through the unsolved cells and place the value for each cell in the 3rd level of each cell. In no particular order. C5R7=4, C6R8=2, C6R4=4, C4R4=7, C4R6=6, C5R6=3, C4R2=4, C5R3=1, C5R2=6, C8R2=7, C7R2=3, C7R3=4, C2R2=1, C2R8=5, C3R8=7, C7R9=9, C9R7=5, C7R7=7, C8R8=4, C7R1=6, C8R1=9, C8R4=3, C9R4=9, C8R5=6, C7R5=5. Now C5R5=2 and C5R4=5. Now your grid should look like Example #23.7 below:
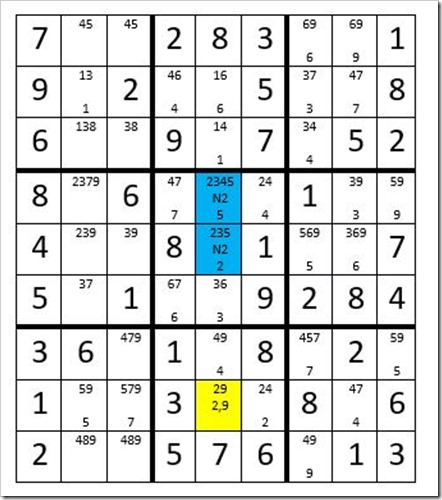
Example # 23.7
|
Example #23.7
We will stop here to consider what we have learned. If C5R8 is a 2, C5R4 cannot be a 2. If C5R8 is a 9, C5R4=5 and is therefore not a 2. C5R8 can only be a 2 or 9. Therefore, C5R4 is not a 2, eliminating the 2 as an option for C5R4. Can we take this further? Yes, continue the track (see Example #23.8 below). C3R7=9, C3R5=3, C2R1=4, C3R1=5, C3R3=8, C3R9=4, C2R9=8, C2R6=7, C2R4=2, C2R5=9, and C2R3=3. You have just solved the puzzle.
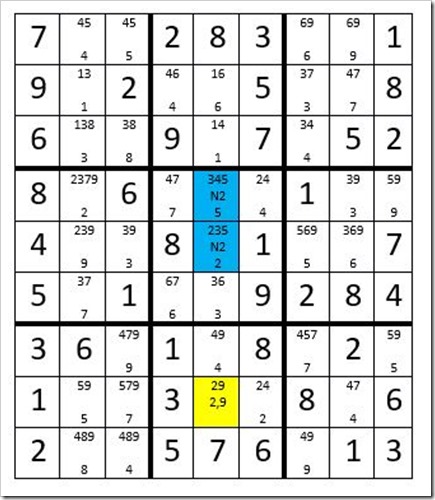
Example # 23.8
|
If we had found a conflict (like a number repeated in a box, column, or row) we could then conclude that the 9 could not be correct, and so C5R8 would have been a 2.
Successful Step 7 exercises eliminate options, but do not always produce a solved puzzle. Sometimes multiple Step 7's are required to solve a puzzle depending on the puzzle as well as which cell you select as a starting cell.
Thank you for your interest. May the gentle winds of Sudoku be at your back!
Editor’s note:
(Photo above… Sudoku is for everyone… and never too young to start! )
Do you tackle a Sudoku on your cottage veranda, sailboat cockpit, or at a campsite? TI Life is taking full advantage of Dan LeKander, from Wellesley Island, who is a Sudoku expert and author of “3 Advanced Sudoku Techniques – That Will Change Your Game Forever!”
In January 2016, we published a final article in his original series – but many of us enjoy using “Dan’s Steps,” so when he asked if we would like a puzzle to solve every month … this editor said an enthusiastic… Yes, please!
I suggest you try this relatively difficult puzzle and that you also purchase Dan’s book, “3 Advanced Sudoku Techniques, That Will Change Your Game Forever!”
Most importantly, I ask that you leave comments on any part of his series and throughout the year. Remember when your teacher said – no such thing as a silly question – as we can all learn together.
Dan’s book is available online, amazon.com and on ebay.com.
Purchase of a book includes a 50-page blank grid pad, 33 black and two green tokens, to assist with Step 6.…
Now as we start a whole new year, I want to say THANKS Dan and THANKS to his better half, Peggy LeKander, who helps make sure the article is correct and reads well. What a team!
|
By Dan LeKander
Dan LeKander and his wife, Peggy, have been seasonal residents of Fineview, on Wellesley Island, NY, since 1983. In addition to being a Sudoku addict, Dan explores the 1000 Islands to enjoy the wildlife, beauty and of course, Catch-and Release bass fishing.
[See Jessy Kahn’s Book Review, “3 Advanced Sudoku Techniques…” by Dan LeKander, June issue of TI Life.]
Do you have any suggestions for future articles? You can post on this TI Life issue, or contact me directly at my e-mail address … djlsuniverse@yahoo.com.